Losing it

Here’s a fun question – let’s consider, purely in the abstract, the notion of quickly putting on a lot of weight. If, hypothetically, one were to weigh themselves every day and, conceptually, throw away all of the results which showed an increase in weight, what, in a strictly Platonic sense, are the odds that actually they’re just a fat shit not actually losing any weight?

Simulation

Let’s engage in this fun thought experiment, as ridiculous as it may seem to the better amongst us who eat well and exercise regularly.

Suppose your real weight fluctuates about a mean \mu with a standard deviation \sigma. Then, when measuring your weight on any given day n > 0, suppose the probability density of measuring a weight w is distributed normally as:

\displaystyle{P(w, n) = \frac{1}{\sqrt{2\pi\sigma^2}}\exp{\left(-\frac{(w - \mu)^2}{\sigma^2}\right)}}

i.e. independent of n – there is no overall trend to your weight.

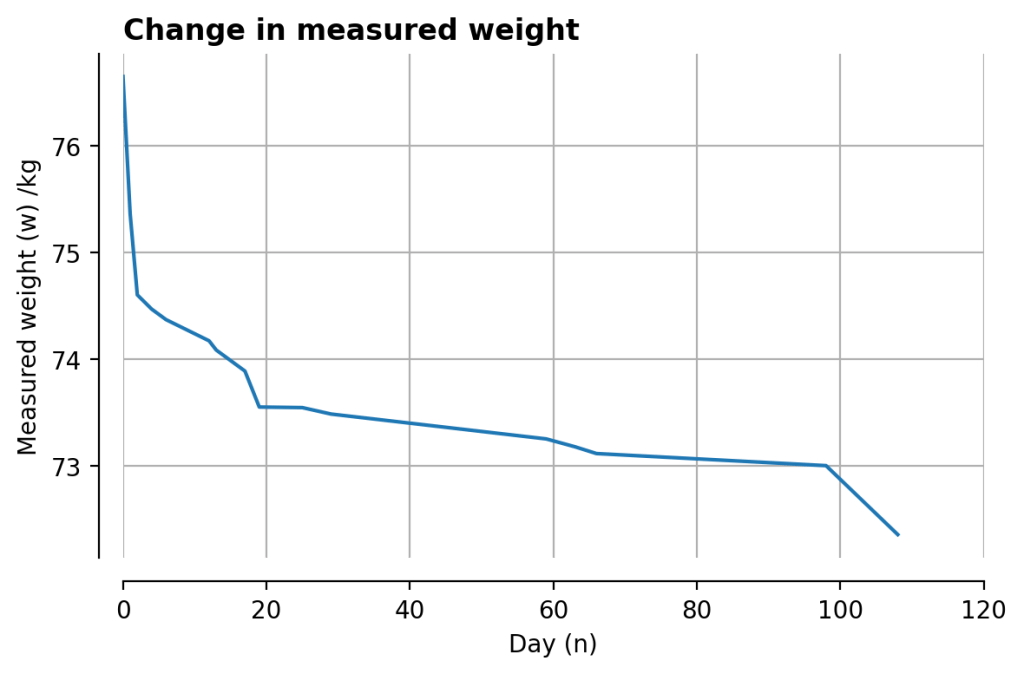
Also suppose that you keep track of your weight, and only record a measurement when it is below your previous record low weight. A sequence of measurements may then look like this, monotonically decreasing:

The y-axis is purely abstract, of course.

Here we’ve simulated the measurement process – every day, draw a sample from P, and if it is low enough, accept it and plot it. It looks great – this hypothetical human has lost several kilograms in just a few months!

It is, sadly, a lie. Here it is overlaid on many similar simulations and their average:

The trend is clearly a rapid initial ‘fall’, followed by an increasingly slow decline – intriguingly similar to the expected weight-loss profile if you were actually caring about your body.

Let’s think about how to model this process in a couple of ways.

Method 1: Iterated expectation

Starting from the beginning, on day 1 the expected value of the measured weight is just (handwaving the integral limits away):

\displaystyle{E(w, n = 1) \equiv w_1 = \int_{-\infty}^{\infty} w \cdot P(w)\,dw = \mu}

Easy enough. What about day 2? This is more interesting – the probability of the actual weight stays the same, but not the reported measurement – the latter is clamped at a maximum of w_1:

\displaystyle{E(w, n = 2) = w_2 = \int_{-\infty}^{w_1} w\cdot P(w)\,dw + \int_{w_1}^{\infty} w_1 \cdot P(w)\,dw}

The particularly eager reader can confirm that this evaluates to

\displaystyle{w_2 = \frac{1}{2}\left(\mu + w_1 + (\mu - w_1)\text{erf}\left(\frac{w_1 - \mu}{\sigma\sqrt{2}}\right) - \sqrt{\frac{2\sigma^2}{\pi}}\exp{\left(-\frac{(w - \mu)^2}{\sigma^2}\right)}\right)}

where the error function \text{erf} is defined as an integral of the gaussian.

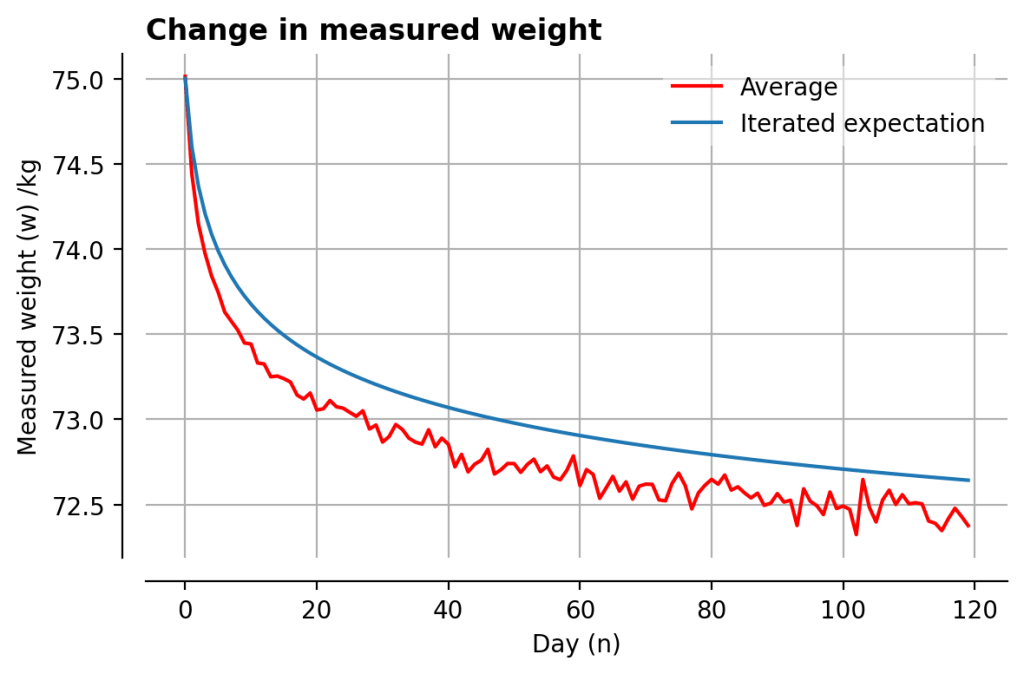
Each day’s measurement is then a function of the previous days – hence ‘iterated expectation’. Let’s see what this looks like compared to the simulation:

It’s not terrible, but it’s not perfect either. The general shape is right, and it might converge to a similar value, but we can do better.

Method 2: Expected minimum

There is another, simpler, way to look at this problem: after n days, the average weight recorded will just be the minimum of all of the measurements so far. Fortunately, there’s a generic way to calculate the distribution of this minimum.

As the distribution of our measurements is constant over time – it exhibits homoscedasticity – for each day is there is a certain probability of measuring a value under W:

\displaystyle{P(w < W) \equiv F(W)}

where F is known as the cumulative distribution function of P. The probability of having a minimum value w_m over W after n days is therefore the probability of all n measurements w_1, w_2, w_3 ... so far being over W:

\displaystyle{P(w_m > W, n) = P(w_i > W)^n} = (1 - P(w_i < W))^n = (1 - F(W))^n

We’re interested in the conjugate case, where w_m < W which is simply

\displaystyle{P(w_m < W, n) = 1 - (1 - F(W))^n}

The probability density distribution of the minimum measured value after n days is then the derivative of this expression:

\displaystyle{P(w_m = W, n) = \frac{d}{dW}\left(1 - (1 - F(W))^n\right) = \frac{n}{\sqrt{2\pi\sigma^2}}\left(\frac{1 - \text{erf}\left(\frac{w_1 - \mu}{\sigma\sqrt{2}}\right)}{2}\right)^{n-1} \exp{\left(-\frac{(w - \mu)^2}{\sigma^2}\right)} }

Phew. We’re not quite there – to get the expected value, we need to integrate this expression again. Unfortunately there’s not a closed form (as far as I can tell), but we can still do it numerically:

Bang on! Well done us.

Method 3: Obscure Stack Exchanging

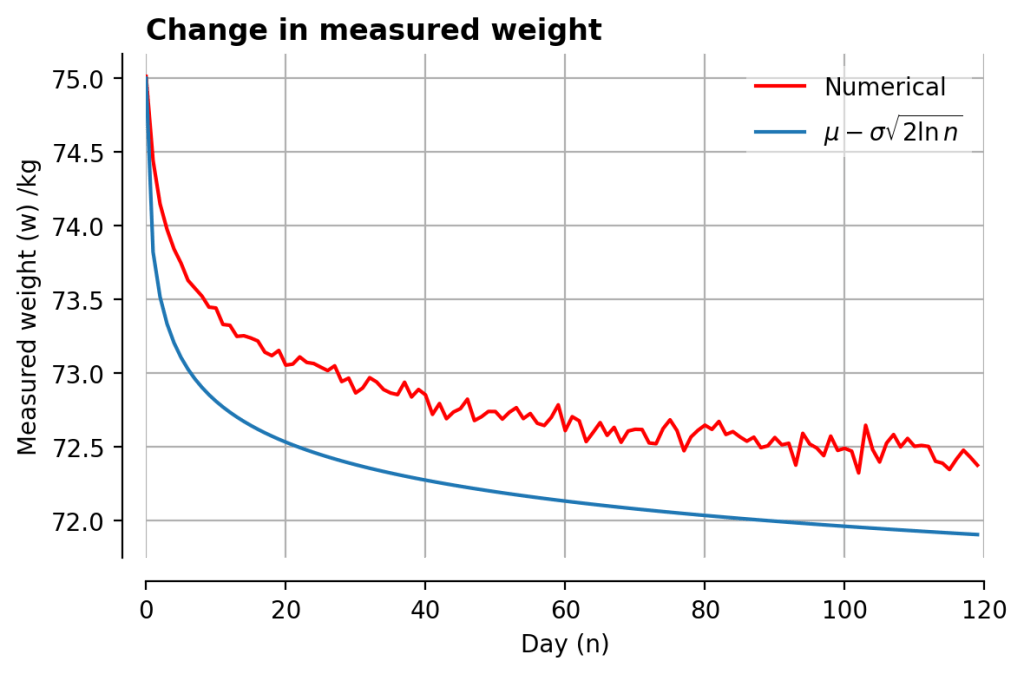
The final method is to go spelunking into the dusty corners of the internet. This comment suggests that a simple approximation is:

\displaystyle{w \approx \mu - \sigma\sqrt{2\ln n}}

Plotting it out, it isn’t too bad! Points to whoever can derive it for me:

And finally, a comparison of all methods:

Is there anything sweeter than a line going straight through some scattered points?

…so?

Although the last method results in the worst approximation, it probably represents a good rule of thumb for figuring out if you’ve actually lost weight:

  • Days 1-10: calculate the mean and standard deviation of your natural weight by measuring it properly every day.
  • Days 10-99: diet, don’t diet, who cares – just keep a record of your minimum weight so far. We all know careful record keeping is better for the body than any amount of quinoa anyway.
  • Day 100: after 90 days, \sqrt{2\ln 90} \approx 2.9999 (yep, 4 nines!), so if you are 3 or more standard deviations below your starting weight, you’ve probably smashed it. Well done! Celebrate by doing some more maths.

One thought on “Losing it”

  1. Cool post!! I never thought about it haha, I guess the same can be said from the other perspective, ie: you only record your maximum weight instead of the minimum. So maybe I’m not getting fat, it’s just a statistical artefact šŸ™‚

    I have a question about your method. Which $\sigma$ did you choose for your distribution? I guess the results depend a lot on that since a bigger sigma would make the illusion of losing/winning weight faster.

    Like

    Reply

Leave a comment